Chapter 04
다양한 분류 알고리즘
.
이제부터 정신 차리고 따라가야 한다..
최소한 이해라도 하려면
04-1 로지스틱 회귀
내가 <로지스틱 회귀>라는 것을 처음 보게 된 것은 한 딥러닝 입문 책이었다.
그 책에서는 가장 먼저 선형 회귀를 앞세워 보여주면서
이어 로지스틱 회귀를 설명했다.
당시에는 전혀 이해되지 않았는데 사실 지금도 쉽게 이해되지 않는다.
로지스틱도 선형 회귀만큼 중요한가보다.
우리가 '분류'라는 작업을 할 때는 근거가 있어야 한다.
주로 그 근거는 각 데이터의 특성에서 따온다.
우리는 그 특성들이 얼마나 뚜렷한가의 차이로 분류한다.
즉, 확률로 표현할 수 있다.
.
앞서 겪었듯 충분히 학습된 선형 회귀는 예측에 신뢰도가 높다.
각 데이터의 특성을 기준으로
패턴을 학습해 하나의 함수로 그룹을 만들 수 있다.
즉, 선형회귀로 grouping하면 정확도가 매우 높을 것이다.
로지스틱 회귀는 이름은 회귀이지만 분류 모델이다.
선형 회귀와 마찬가지로 선형 방정식을 학습하지만
그 결과 값을 시그모이드 함수(로지스틱 함수)에 통과시켜
0~1까지의 결과 값을 반환한다. #(04-1) 2번 문제

z는 모델이 학습한 선형 방정식이다.
z값이 클수록 '타깃'데이터에 가깝다.
따라서 시그모이드 함수를 적용하면 타깃데이터일 확률이 나온다.
여기서 1에 대해 결과값을 빼면 비교대상일 확률이 나온다.
즉, 이진분류에 적합한 모델이다.
(타깃데이터이거나 아니거나)
.
물론 다중 분류에도 사용할 수 있다.
회귀 파트에서와 같이 정규화(규제)를 한다면 여러 클래스로 분류할 수 있다.
우리가 사용하는 사이킷런의 LogisticRegression 클래스는 릿지 회귀와 같이 <계수의 제곱>을 규제한다.
다중 분류는 클래스마다 z값을 계산해 내고 이진 분류와 달리 소프트맥스 함수를 사용하여 확률을 구한다.


각 z값에 대한 지수 함수를 계산해 모두 더한 후 분모로 사용하면 각 데이터의 확률이 된다.
여러 선형 방정식의 출력값을 0~1 사이로 압축(정규화)하고 전체 합이 1이 되도록 만든 것이다.
(확률의 총합 = 1)
04-2 확률적 경사 하강법
지금까지의 모델들은 훈련데이터를 토대로 모델을 평가하고 사용했다.
하지만 만약 훈련데이터가 매일매일 추가된다면?
매일매일 다시 훈련하고 평가하는 과정은 매우 귀찮다.
이를 해결해 줄 대표적인 점진적 학습 알고리즘이 확률적 경사 하강법이다.
.
기본적인 원리는 훈련 세트에서 일정부분의 샘플을 랜덤으로 꺼내
모든 샘플을 사용할 때까지 훈련을 반복하는 것이다.
훈련세트를 추가한다면 그 세트를 다 비울 때까지 또 반복 훈련할 것이다.
이때 꺼내는 양에 따라 다음과 같이 분류할 수 있다.
1개씩 꺼내기 : 확률적 경사 하강법
여러 개씩 꺼내기 : 미니배치 경사 하강법
전부 사용 : 배치 경사 하강법
(신경망 알고리즘에서는 데이터가 너무 많아 무조건 경사 하강법을 사용한다고 한다.)
하지만 지금까지 겪어왔듯 학습을 많이 한다고 다 좋은 게 아니다.
학습을 할수록 모델은 과소적합에서 과대적합으로 변한다.
따라서 과대적합 이전에 조기 종료해야 원하는 모델을 사용할 수 있다.
.
모델이 얼마나 엉터리인지, 얼마나 잘 맞는지 측정하는 기준이 필요하다.
즉, 오차가 최소인 모델을 찾는 손실 함수를 사용한다.
손실 함수가 최소일 때 주로 오차가 최소이기에 쉽게 생각하면 최소인 극소점을 찾으면 되는 것이다.
손실함수는 연속적이며 미분 가능해야 한다.
회귀의 경우 손실 함수로 평균 제곱 오차를 많이 사용한다고 한다.
하지만 로지스틱 회귀의 경우 이 함수를 사용하면
최소가 아닌 극소점에서 조기 종료할 수 있기에 다른 손실 함수를 적용해야 한다.
(모델마다 맞는 손실 함수가 따로 있다)
.
로지스틱 손실 함수라고 부르는 다음 함수를 사용한다.
타깃이 1일 때(양성 클래스) : -log(예측 확률)
타깃이 0일 때(음성 클래스) : -log(1-예측 확률)
(이진 크로스엔트로피 손실 함수라고도 부른다)
다중 분류의 경우 크로스 엔트로피 손실함수를 사용한다.
이렇게 경사 하강법을 이용해 손실함수에 적용하면
어느 순간 원하는 모델이 만들어진다.
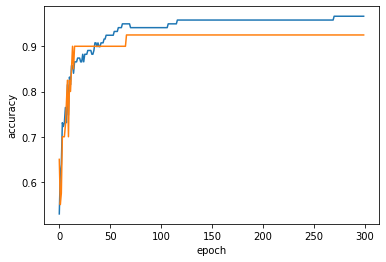
훈련 횟수 즉, 에포크 횟수에 따라 과대 적합 혹은 과소 적합이 될 수 있다.
적절한 에포크 값은 이전 회귀를 규제할 때 alpha값을 찾는 과정과 비슷하다.
다음과 같이 훈련 세트와 테스트 세트를 에포크에 대한 정확도에 비교하면 된다.
4장 정리
1. 로지스틱 회귀 모델을 사용하면 대량의 데이터를 확률을 이용해 효과적으로 분류할 수 있다.
2. 훈련 세트를 최신화해 계속 적절한 모델을 찾아야 한다면 확률적 경사 하강법을 이용할 수 있다.
3. 확률적 경사 하강법에는 맞는 손실 함수를 이용하며 에포크 횟수를 조절해 원하는 모델을 만들 수 있다.
.
.
5장에는 트리 알고리즘이 나온다..
노드 개념이 아직 익숙하지 않는데 잘 이해되면 그것만으로도 좋을 것 같다..
'Programming > 혼공머신 8기.py' 카테고리의 다른 글
| 혼자 공부하는 머신러닝 + 딥러닝 [6주차]_fin (0) | 2022.08.15 |
|---|---|
| 혼자 공부하는 머신러닝 + 딥러닝 [5주차] (0) | 2022.08.10 |
| 혼자 공부하는 머신러닝 + 딥러닝 [4주차] (0) | 2022.07.27 |
| 혼자 공부하는 머신러닝 + 딥러닝 [2주차] (0) | 2022.07.13 |
| 혼자 공부하는 머신러닝 + 딥러닝 [1주차] (0) | 2022.07.07 |